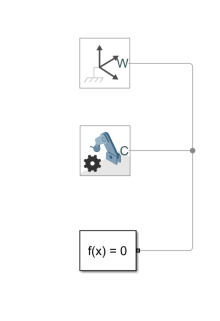
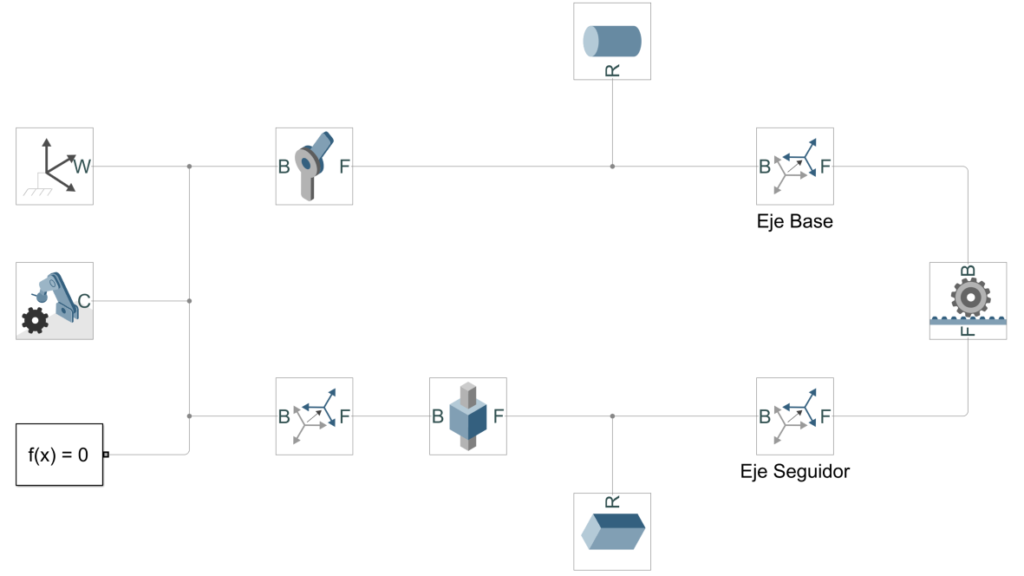
Para representar las ecuaciones diferenciales en simulink debe seguir los siguientes pasos:
- Identificar la derivada de mayor orden y agregar bloques integradores.
- Resolver para la derivada de mayor orden.
- Representar el lado derecho de la ecuación
Modelo matemático
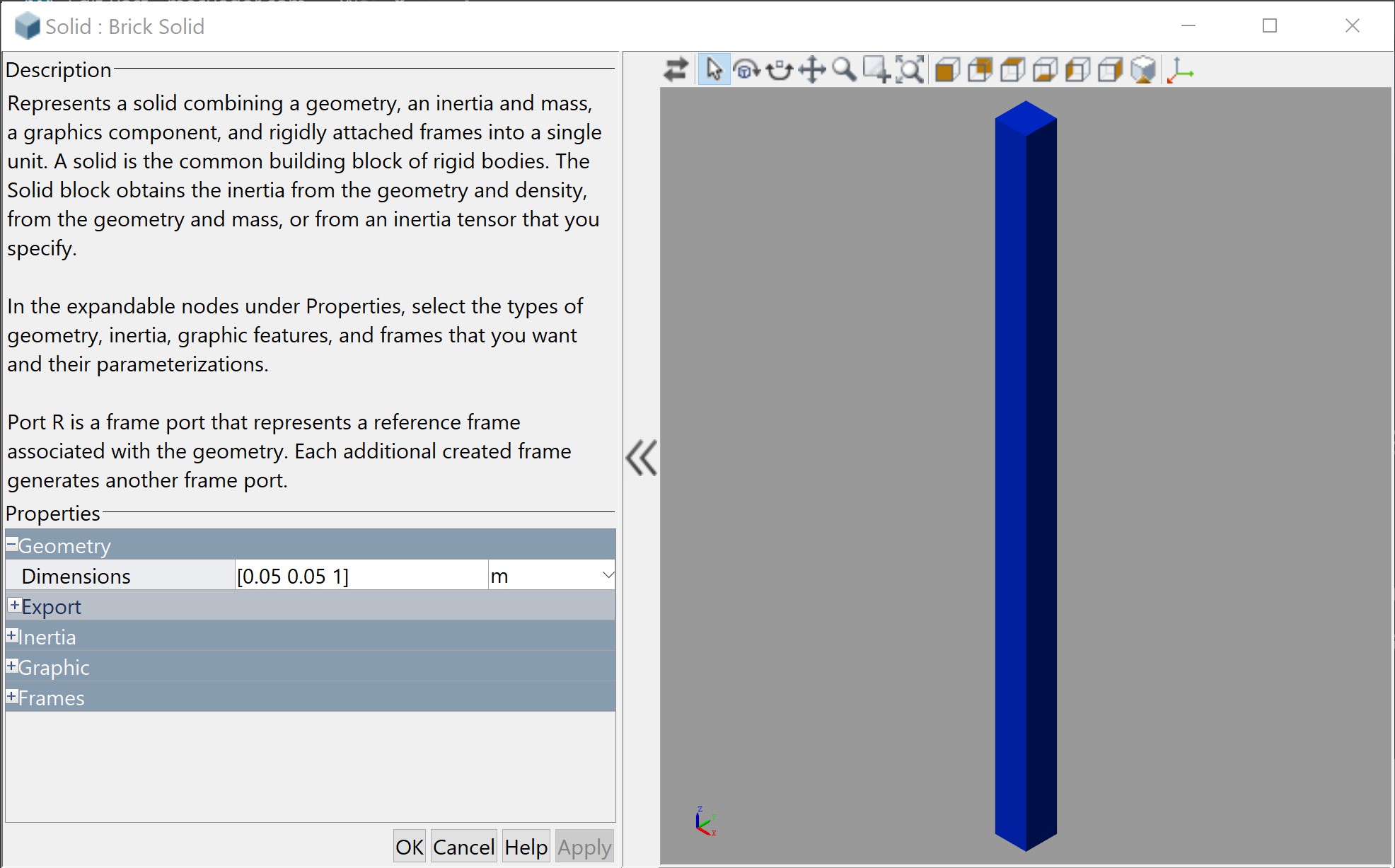
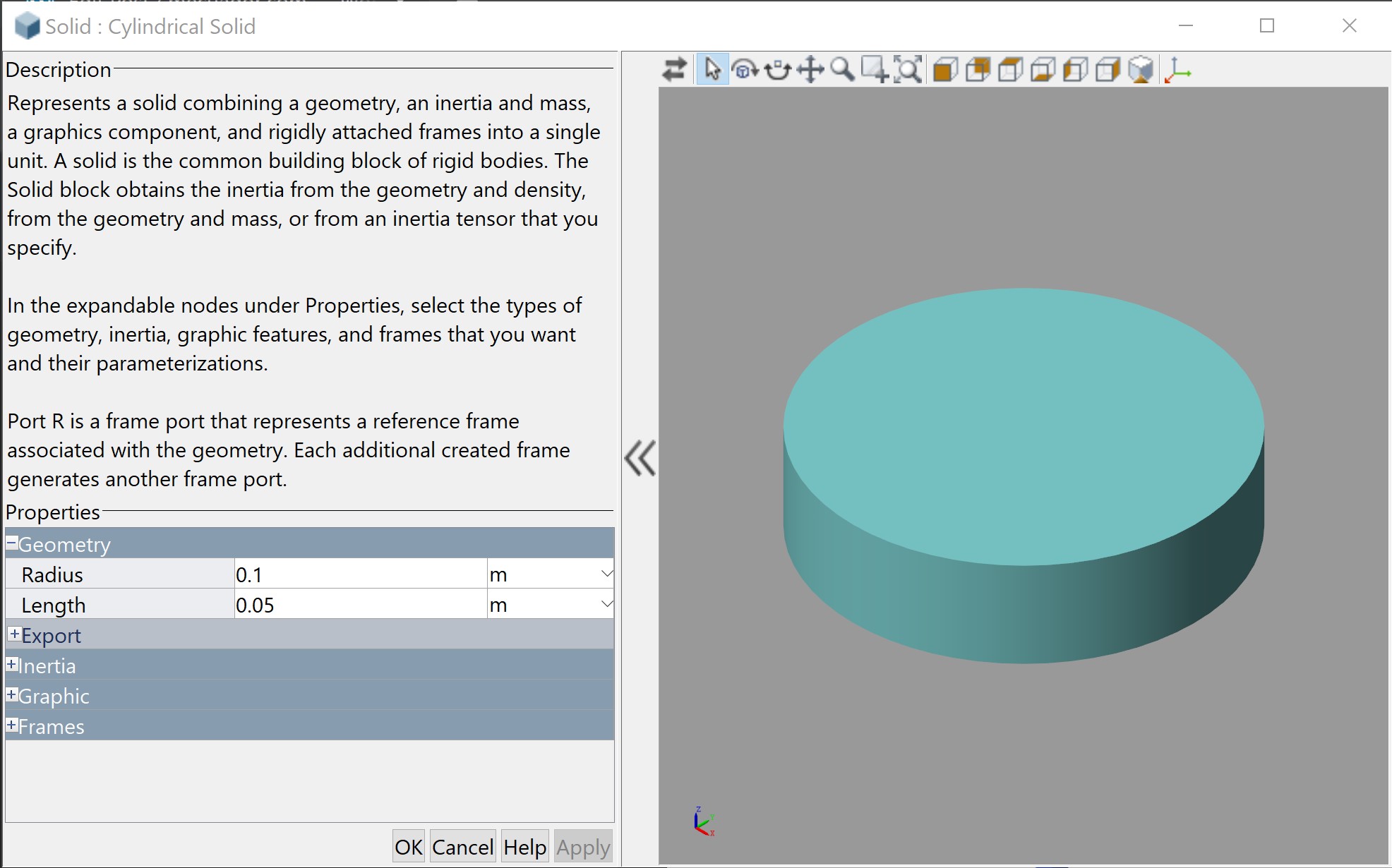
Considere el sistema de la figura en el cual se puede apreciar que se aplica un torque en un extremo del sistema, mientras que al otro extremo se encuentra un amortiguador torsional de coeficiente C_T.
La polea tiene un momento de inercia I y su radio tiene el valor R. La masa que está siendo levantada tiene un valor de m.
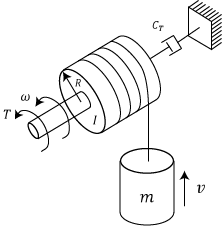
El modelo matemático del sistema es el siguiente:
T*R = (I+m*R^{2})*x^{\prime\prime}+C_T*x^{\prime}En este tutorial se utiliza la versión de matlab 2021b.
Representación del modelo matemático
Conectar integradores
En este ejemplo la derivada de mayor orden es de segundo orden; por lo tanto, se deben agregar dos bloques integrador (Integrator).

Conecte los integradores en serie, y agregue conectores tanto al inicio como al final de los bloques.

Puede agregar etiquetas a los conectores dando doble click en cada uno de ellos para indicar las variables utilizadas.
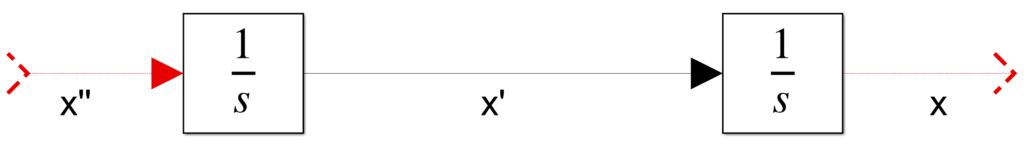
Resolver para la derivada de mayor orden
Representar el lado derecho de la ecuación
Ganancias
Los factores deben ser representados por medio de bloques de ganancia(gain).
Primero, se representará el termino C_T*x^{\prime}
El factor C_T está multiplicando a la variable x^{\prime} ; entonces, en el bloque de ganancia se debe utilizar C_T. La entrada debe ser conectada al conector x^{\prime} .
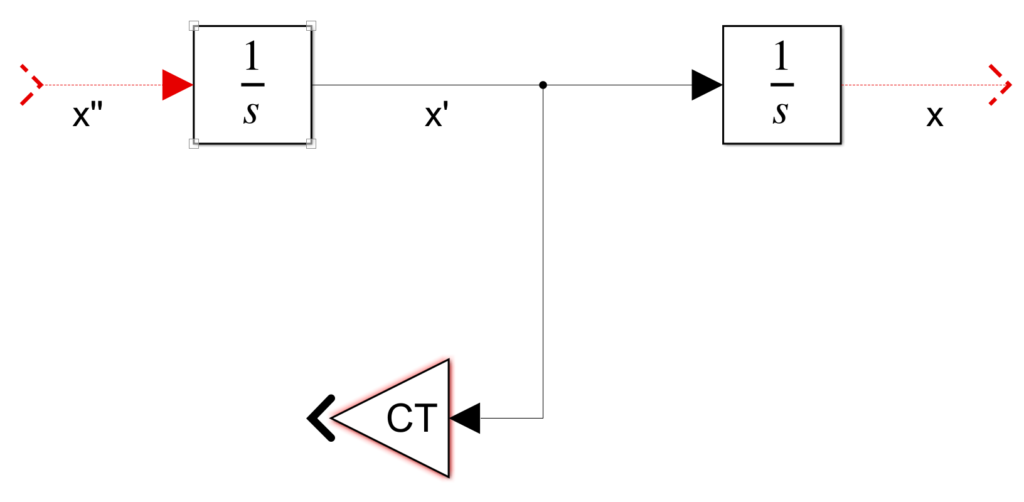
Otro factor es \frac{1}{(I+m*R^{2})} , el cual está multiplicando a todo lo que se encuentra en el lado derecho de la ecuación. Para este senecesita un nuevo bloque de ganancia. Por el momento no será conectado. Si el bloque de ganancia indica -K-, significa que no puede mostrar todo el contenido. Esto se soluciona aumentando el tamaño del bloque.
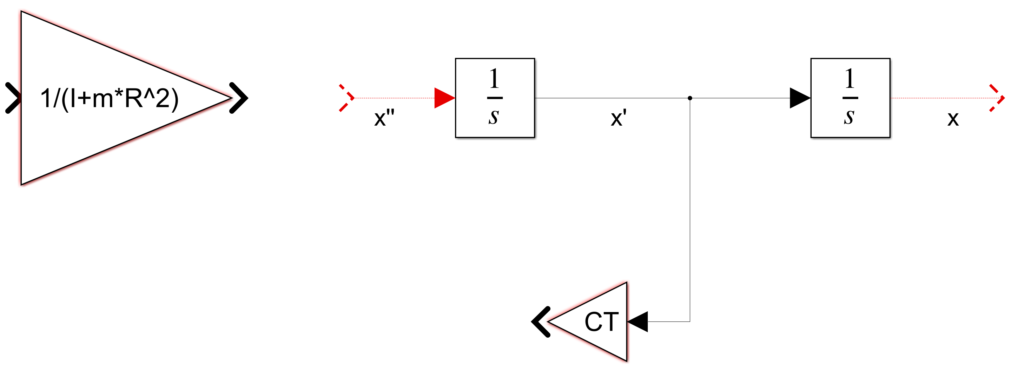
Para el torque aplicado T se utilizará una entrada del tipo escalón. Para esto se requiere agregar el bloque «Step». Adicional, se necesita un bloque de ganancia para el factor R
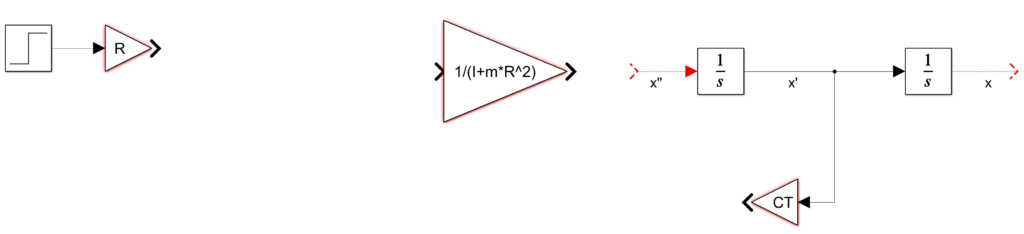
Bloque sumador
Para completar el modelo se necesita un bloque sumador y poder completar la operación del lado derecho de la ecuación. Agregue el bloque sumador(Add) y conecte la salida de la ganancia con el el factor C_T. También, conecte la salida de la ganancia R .
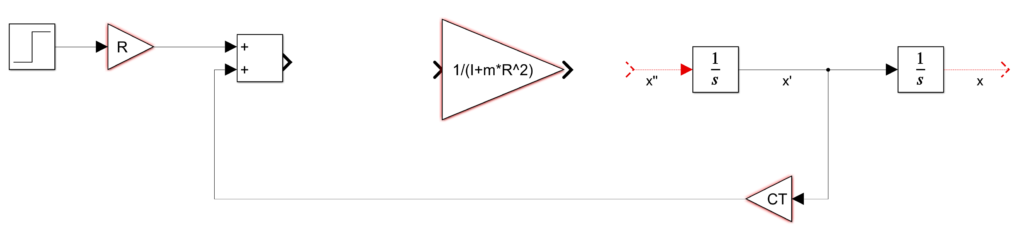
Se puede observar que se tienen un término positivo y un término negativo. Para ajustar esto en el bloque sumador. Se debe dar doble click en el bloque para editar sus propiedades.
Configure el bloque de la siguiente forma y acepte los cambios.
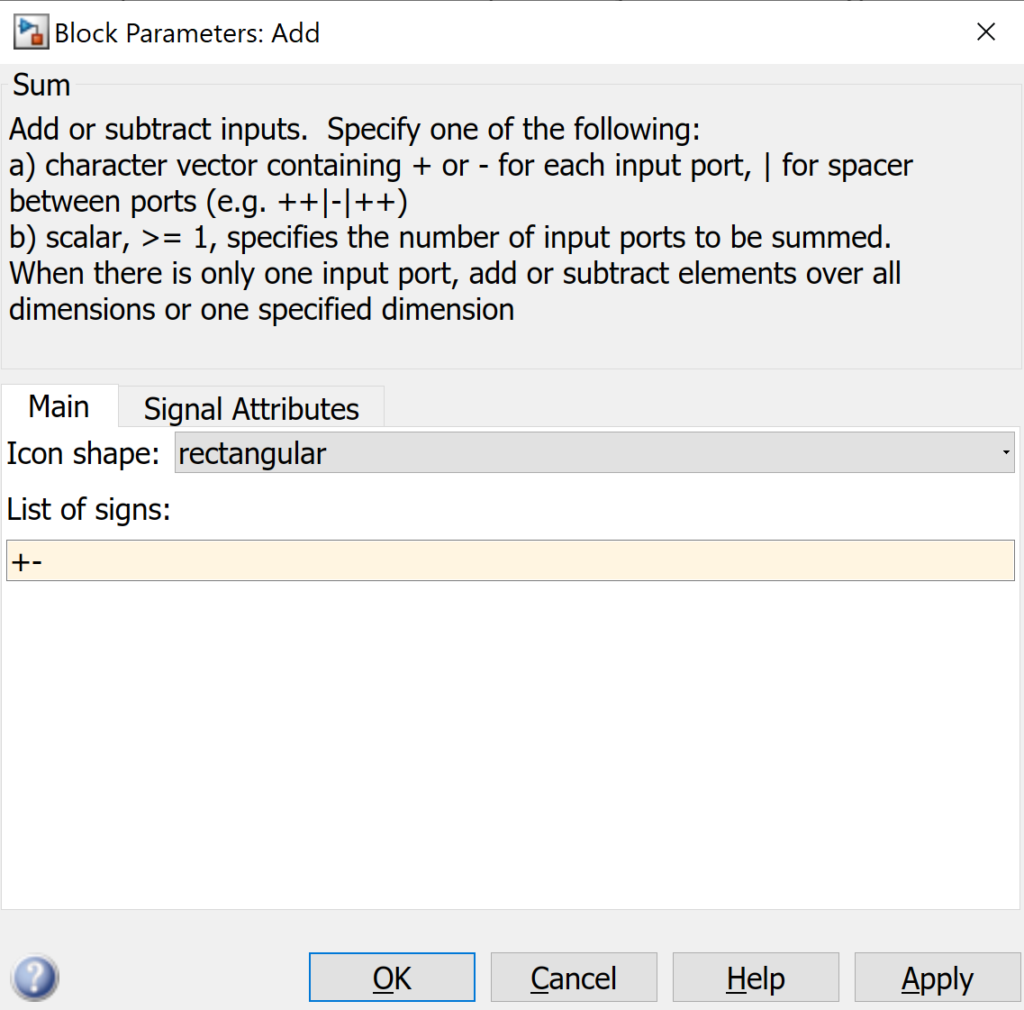
Como resultado se puede observa que el bloque sumador tiene ahora una entrada con signo negativo
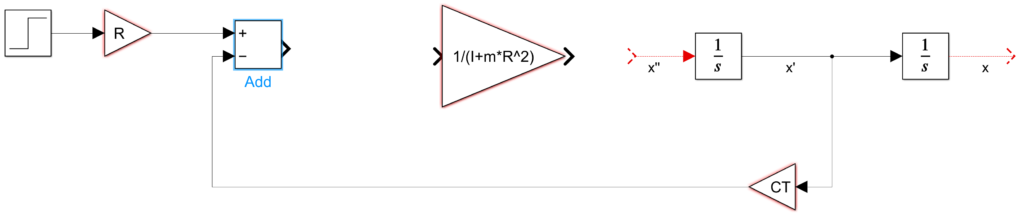
Antes de realizar las conexiones faltantes se muestra las etiquetas de los conectores de las salidas de las ganancias.
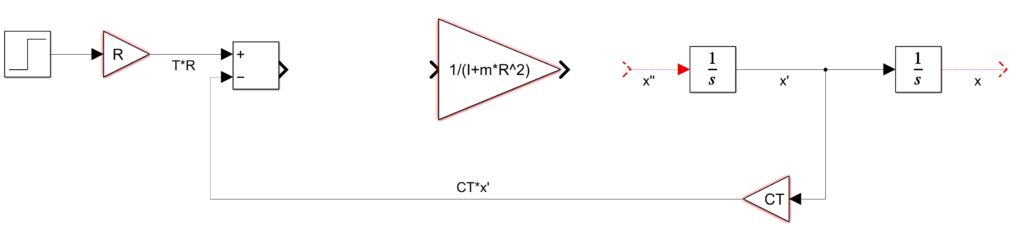
La salida del sumador se conecta a la entrada de la ganancia \frac{1}{(I+m*R^{2})} .
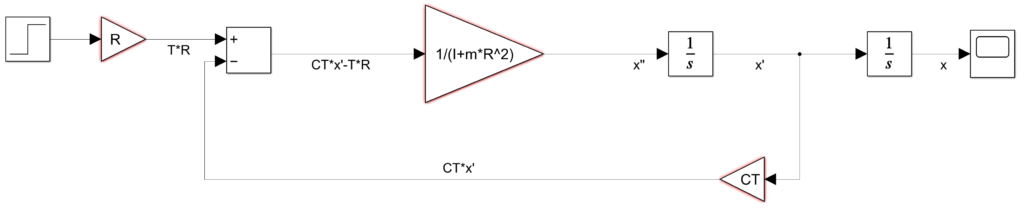
Se puede observar la salida del bloque sumador (Add) representa la diferencia presente al lado derecho de la ecuación y al ser multiplicado por la ganancia se obtendría x^{\prime\prime}. Para poder medir la posición de la masa se utiliza un scope conectado a la salida del último integrador.
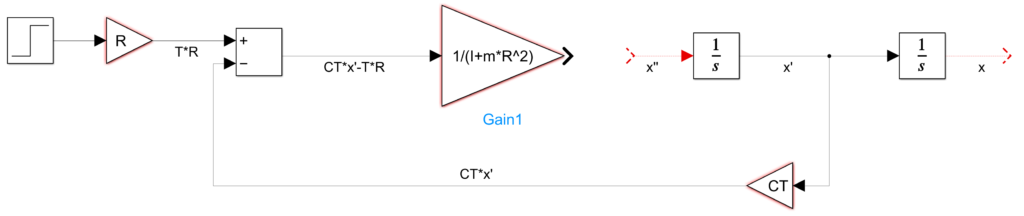
A la salida de la ganancia de mayor tamaño se tiene la expresión \frac{1}{I+m*R^{2}}*(C_T-T*R) lo cual equivale a x^{\prime\prime}
Declaración de variables
Al momento se puede observar que las ganancias tienen un borde rojo indicando que existe un error. Esto es debido a que la constantes no han sido definidas.
Ingrese en las propiedades del modelo.
Configure los siguientes datos del modelo en el Callback InitFcn:
R = 0.2\,m \\I = 0.8\,kg \cdot m^2 \\C_T=0.1\,N \cdot m \cdot s \\m = 40\,kgDe esta forma las variables se quedan guardadas en el modelo y se cargarán cuando se ejecute el modelo.
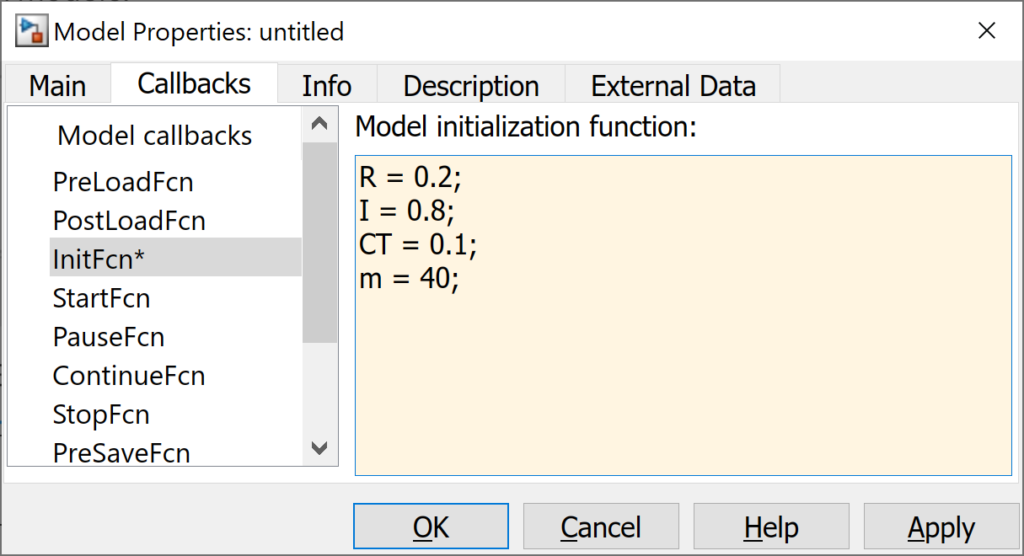
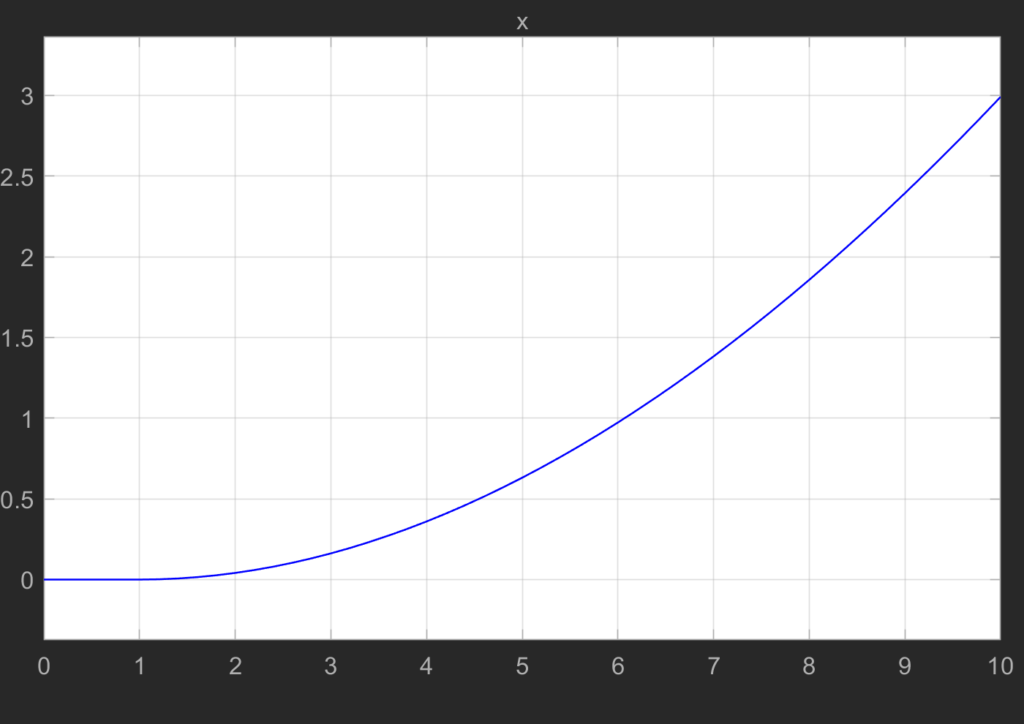
Aplique los cambios y ejecute la simulación del modelo.
Debe obtener el siguiente resultado de la posición del objeto de masa m .
Palm, W. J. (2005). System dynamics(2nd ed). Boston: McGraw-Hill Higher Education.